Fundamentos de Computação Gráfica - INF2608 - 2013.1
Trabalho 1 - Processamento de Imagem
O objetivo deste trabalho era implementar um programa simples que permitisse a visualização de imagens e a aplicação de filtros e transformações sobre as mesmas.
As funcionalidades implementadas foram:
Filtros: Gaussiano, Média, Mediana, Laplaciano e Sobel.
Transformações: Binarização, Brilho, Contraste, Codificação Gama, Espelhamento, Inverter Cores e Tons de Cinza.

Tela da aplicação com uma imagem inicial carregada.
Arquitetura
A aplicação é composta pelas classes MainWindow e ImageHandler. A MainWindow implementa a janela principal na forma como está estruturada e trata os eventos da interação do usuário sobre ela. Alguns eventos como o de aplicação de filtros de imagem, por sua vez, são tratados de forma a repassar a requisição dos cálculos para a classe específica de manipulação de imagens, ImageHandler.
A classe ImageHandler implementa os métodos responsáveis pelos filtros e transformações que compõem este trabalho.
Implementação
FILTROS
GAUSSIANO: É um filtro passa-baixa, linear no domínio espacial. Ele suaviza a imagem, dando uma característica de leve "borramento", sendo o mais adequado para o tratamento do chamado ruído gaussiano "branco", processo estocástico com média zero. A máscara que representa esse filtro no domínio espacial da imagem digital é a matriz 3x3 abaixo:
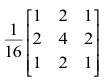
Apenas por uma questão de simplificação, as bordas da imagem não foram tratadas nesta implementação.
 ._.
._.
Imagens processadas com filtro Gaussiano. A primeira foi suavizada. Na segunda o ruído "branco" foi amenizado.
MÉDIA: É um filtro passa-baixa, linear no domínio espacial. Ele suaviza a imagem, dando também uma característica de leve "borramento". A máscara que representa esse filtro no domínio espacial da imagem digital é a matriz 3x3 abaixo que, com soma de pesos igual a 1, fornece a média aritimética dos pixels da vizinhança.
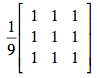
Apenas por uma questão de simplificação, as bordas da imagem não foram tratadas nesta implementação.
MEDIANA: É um filtro passa-baixa, não linear no domínio espacial. Sua característica é a de suavizar a imagem, porém minimizando bastante o efeito de "borramento". A máscara utilizada nesta implementação foi de dimensão 3x3, sendo que pode-se também optar por usar outras dimensões. Quanto maior a dimensão, maior será o efeito de suavização. O processo consiste em ordenar os pixels da vizinhança e o valor do pixel central passa a ser o valor mediano dos vizinhos.
Este filtro é ideal para o tratamento de ruídos do tipo "sal e pimenta".
Apenas por uma questão de simplificação, as bordas da imagem não foram tratadas nesta implementação.

Imagem original e imagem processada com filtro de Mediana.
LAPLACIANO: O Laplaciano de uma função bidimensional f(x,y) é uma derivada de segunda ordem definida por:
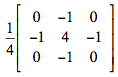
Apenas por uma questão de simplificação, as bordas da imagem não foram tratadas nesta implementação.

Imagem original e imagem processada com o operador Laplaciano.
SOBEL: É um filtro passa-alta, não linear no domínio espacial. Tem a propriedade de detectar mudanças bruscas no nível de cinza e realçar as arestas de uma imagem, correspondentes à alta frequencia da função original. Pode-se obter a detecção de arestas independente da direção, fazendo uma filtragem nas direções ortogonais, vertical y e horizontal x, onde os dois resultados constituem as componentes de um gradiente.
O operador Sobel é dado pela seguinte expressão:
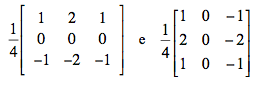

Imagem original e imagem processada com filtro de Sobel.
TRANSFORMAÇÕES
BINARIZAÇÃO: Binarizar uma imagem significa atribuir apenas um entre dois valores possíveis para cada pixel, branco ou preto. Para isso deve-se primeiro convertê-la para tons de cinza, para então aplicar um dos métodos de binarização vistos em aula. A implementação consiste em achar um limiar(threshold), que denota o valor de pixel que minimiza a variância entre os tons de cinza, sendo este o valor que definirá a qual classe(branco ou preto) pertence cada pixel. O método usado neste trabalho para determinar o limiar foi o método de Otsu.
Após o cálculo do limiar percorre-se toda a imagem testando o seu valor contra o valor de cada pixel, o que definirá se ele terá valor zero ou 255.
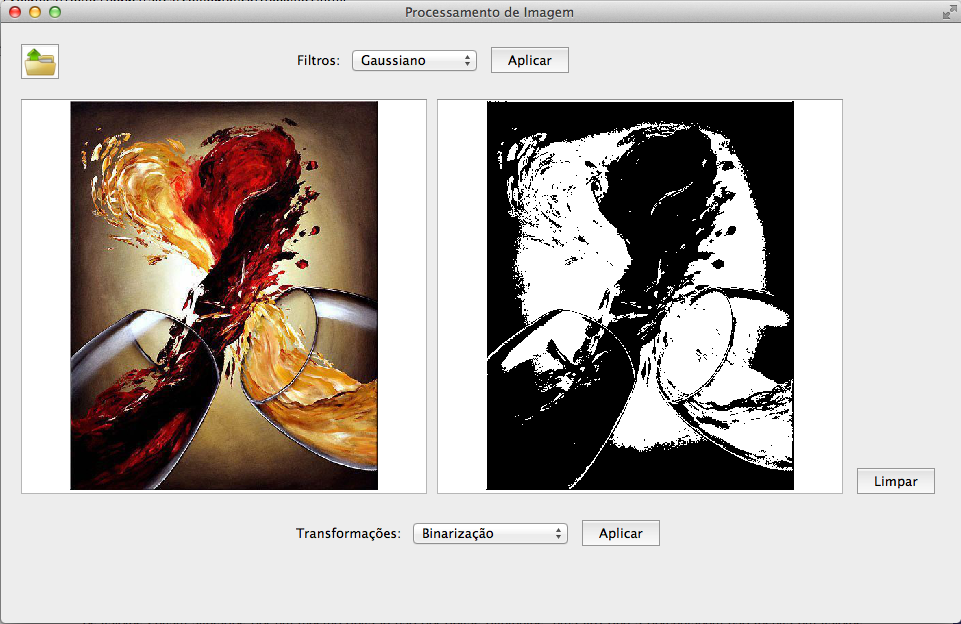
Imagem original e imagem após binarização.
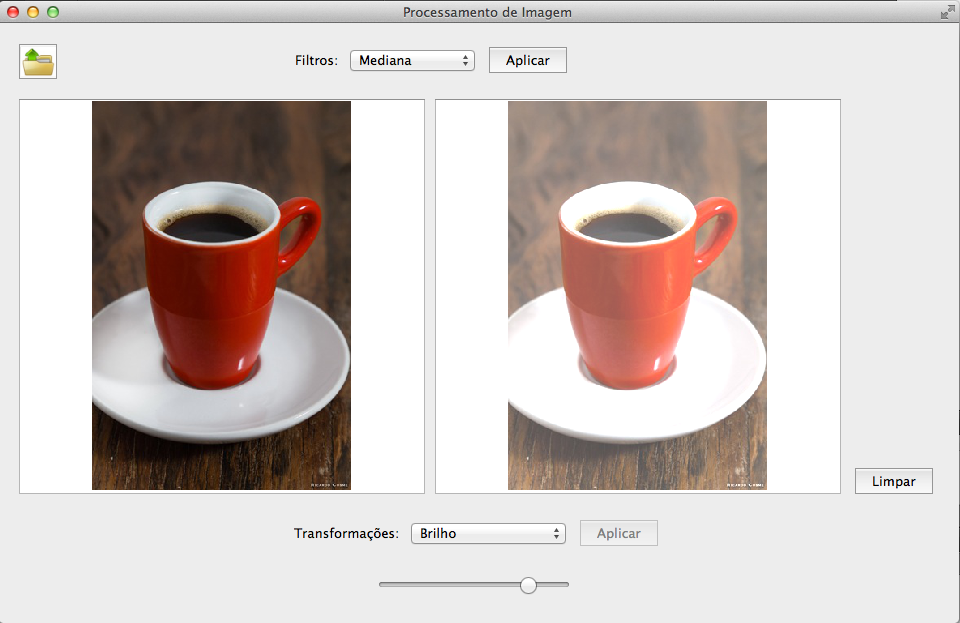
BRILHO: Para alterar o brilho desliza-se o slider da janela, que está entre os valores -128 a 128. O valor corrente do Slider é somado (ou diminuído) aos valores R,G e B de cada pixel da imagem. Dado um histograma para cada canal de cor, onde o eixo x dispõe os valores de 0 a 255 (pois trata-se de uma imagem de 8 bits por canal), e o eixo y é a quantidade de pixels da imagem em cada intensidade, na prática ocorre que o aumento do brilho desloca cada histograma para a direita, pois está aumentando a intensidade do tom da cor. Como cada canal está sofrendo o mesmo aumento, a imagem fica mais clara. Em um histograma de luminosidade, mais tons estariam se deslocando para a região dos "highlights". O análogo acontece para a diminuição do brilho.
O histograma de luminosidade é mais preciso que o histograma R,G,B na descrição da distribuição do brilho (ou luminosidade), pois a luminosidade leva em conta a diferença de sensibilidade do olho humano para o azul, verde e o vermelho. O histograma de luminosidade é construído de forma análoga ao anterior, mas a intensidade do pixel no eixo x é a intensidade luminosa, que é obtida pela a soma de contribuições diferentes de cana canal: Y = 0,2126*R + 0,7152*G + 0,0722*B
Referências: http://www.cambridgeincolour.com/tutorials/histograms1.htm
http://www.cambridgeincolour.com/tutorials/histograms2.htm
 ._.
._.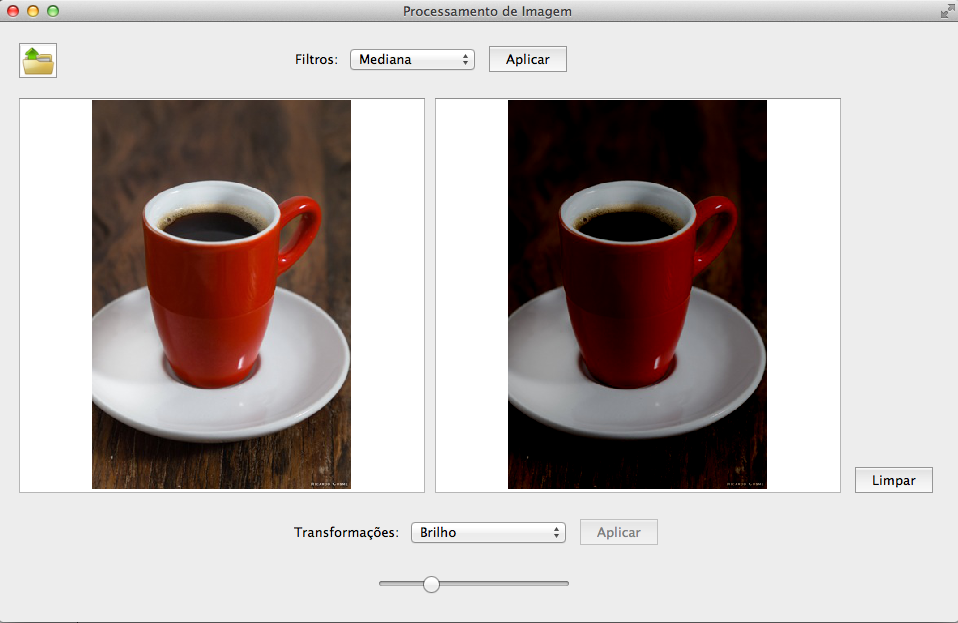
Imagens com aumento e diminuição do brilho respectivamente.
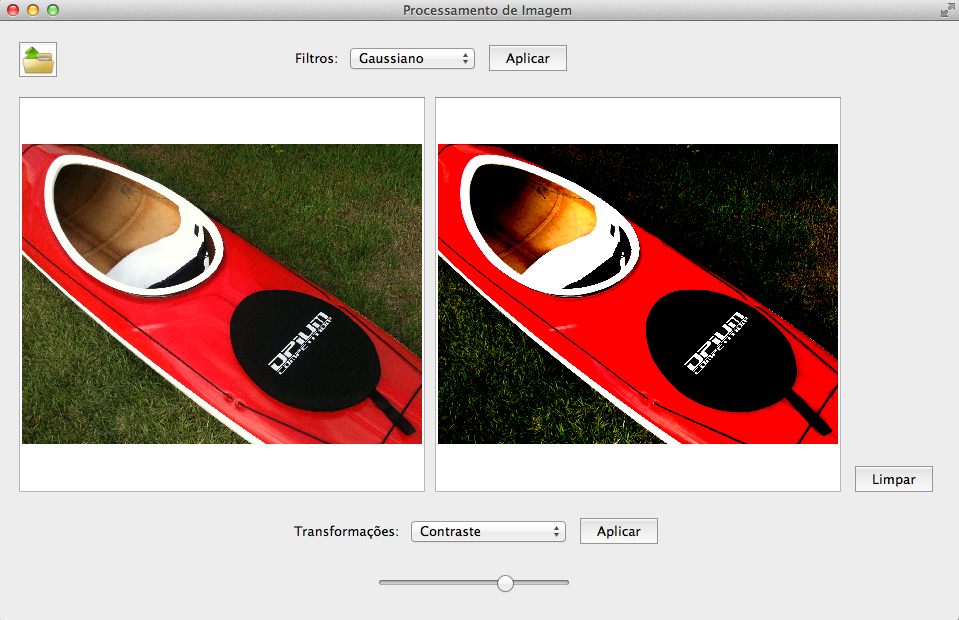
CONTRASTE: Um histograma pode também representar a quantidade de contraste. O contraste mede a diferença de luminosidade entre as áreas claras e escuras em uma imagem. Quando aumentamos o contraste, o histograma se estende, denotando que uma quantidade de pixels de tons médios(mid-tones) se reajustaram para tons escuros e claros. Ou seja, aumentou-se a quantidade de pixels nas regiões mais escuras e mais claras. O análogo acontece para a diminuição do contraste.
Neste trabalho o contraste é controlado por um Slider, que varia de -128 a 128 e o cálculo foi extraído de algumas fontes na Internet.
Primeiro determina-se o Nível de Contraste: contrastLevel = ( (100 + sliderVal) / 100 )^2
Depois, para cada canal de cor faz-se: red = ( ((red/255 - 0.5) * contrastLevel) + 0.5 ) * 255
 ._.
._.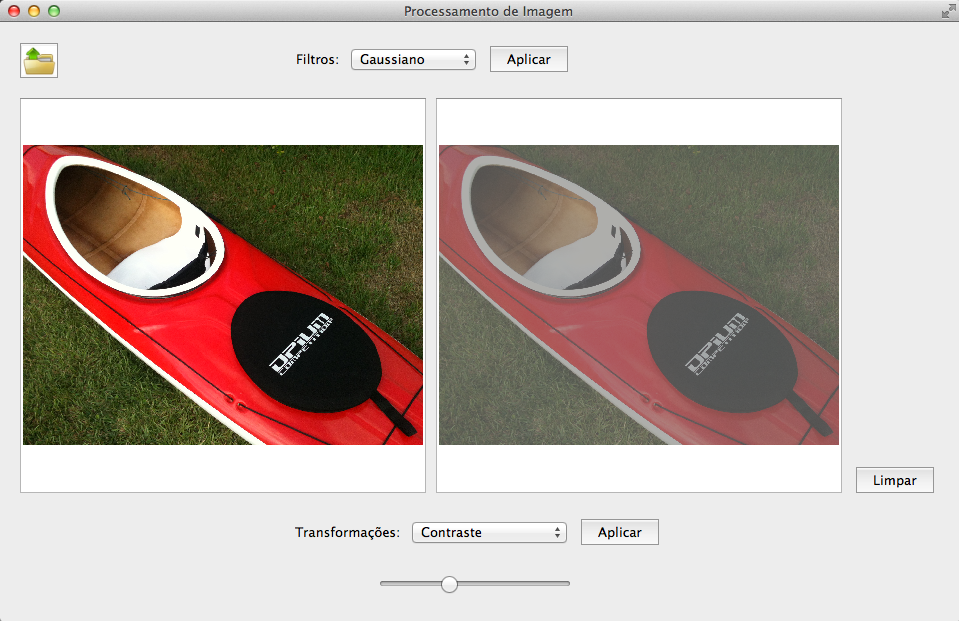
Imagens com aumento e diminuição do contraste respectivamente.
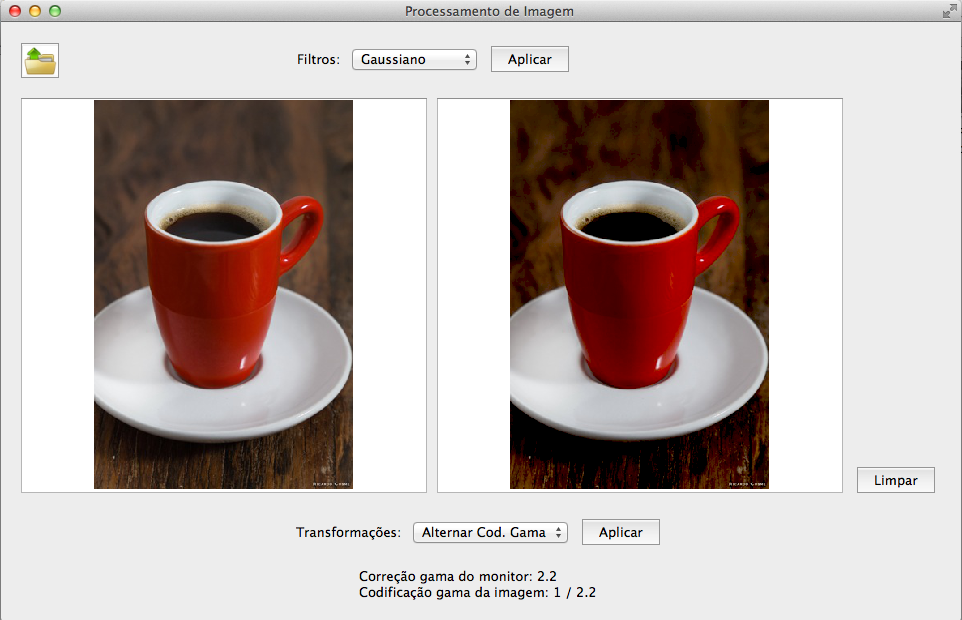
ALTERNAR CODIFICAÇÃO GAMA: O Gama define a relação entre o valor numérico de um pixel e sua real luminância. A aplicação da codificação gama é na gravação da imagem, e não na sua exibição. Quando uma imagem digital é salva ela é "codificada com gama"(gamma-encoded), de modo que o dobro de um valor em um arquivo de imagem, corresponda ao que se percebe como duas vezes mais brilhante. O segundo passo, o gama de exibição(display gamma), é automaticamente realizado pelos monitores. Uma imagem codificada com gama deve sofrer uma "correção gama" simétrica quando é visualizada, que efetivamente a converte de volta para a luz da cena original.
Neste trabalho, a funcionalidade implementada ao redor do tema 'Gama', foi a opção de se alternar entre a imagem por padrão codificada com gama 1/2.2 e a remoção desta codificação, simulando uma imagem raw, com um gama linear (1.0). Para isso, eleva-se o valor do pixel a 2.2. Vale lembrar que o gama de exibição(display gamma) do monitor usado é de 2.2. Ou seja, se desfizermos a codificação padrão(1/2.2), a imagem passa a ter a codificação linear (1.0) e, como a correção do monitor é 2.2, a codificação e a exibição não se cancelam e a imagem aparece mais escura, pois a correção do monitor está mais alta que a codificação da imagem.
Informações mais detalhadas sobre todo o processo de "Correção Gama" podem ser econtradas no link abaixo:
Referência: http://www.cambridgeincolour.com/tutorials/gamma-correction.htm
 ._.
._.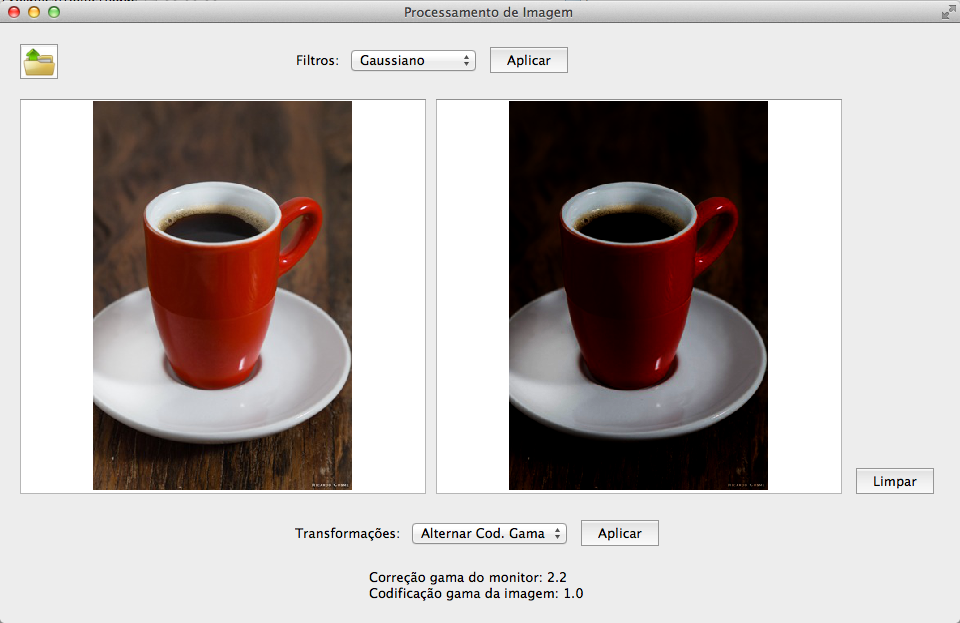
Imagens após mudanças na codificação gama. A primeira mostra a imagem sem alteração no gama original. A segunda, mostra a "remoção" da codificação original (1/2.2), ao passo que o monitor tenta aplicar a correção simétrica de 2.2
ESPELHAMENTO: O espelhamento de imagem nesse trabalho foi realizado em torno do eixo vertical, de forma que, para cada ponto da imagem, a altura é mantida e o índice no eixo da largura é trocado com o seu "mesmo índice" no lado oposto.
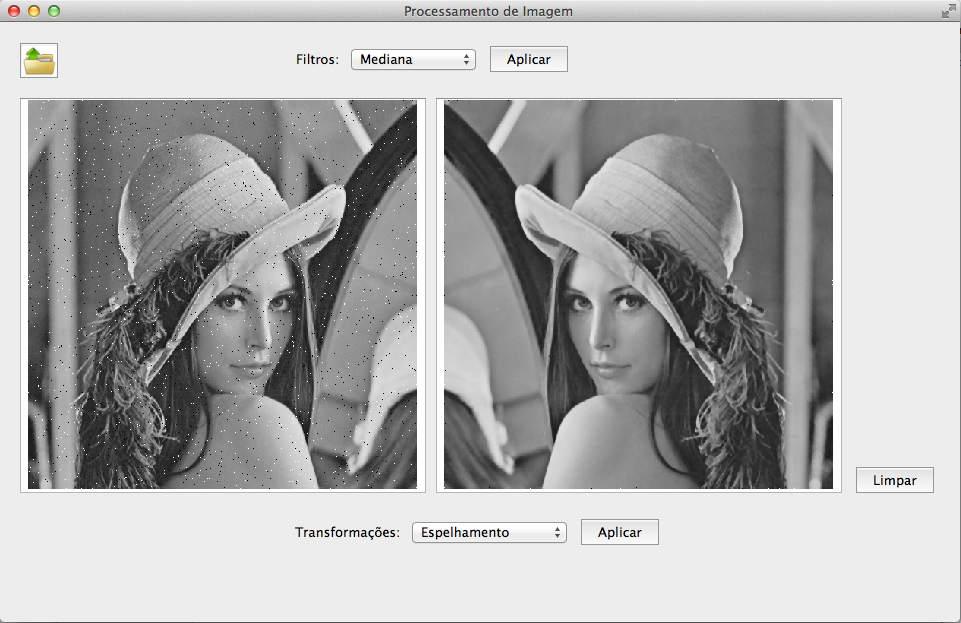
Imagem original e imagem após filtro de mediana e espelhamento.
INVERTER CORES: A inversão de cores consiste em aplicar a subtração 255-red, 255-green, e 255-blue, para cada pixel da imagem. Ou seja, inverter os componentes R,G e B, fazendo o máximo de sua escala menos seu valor original.
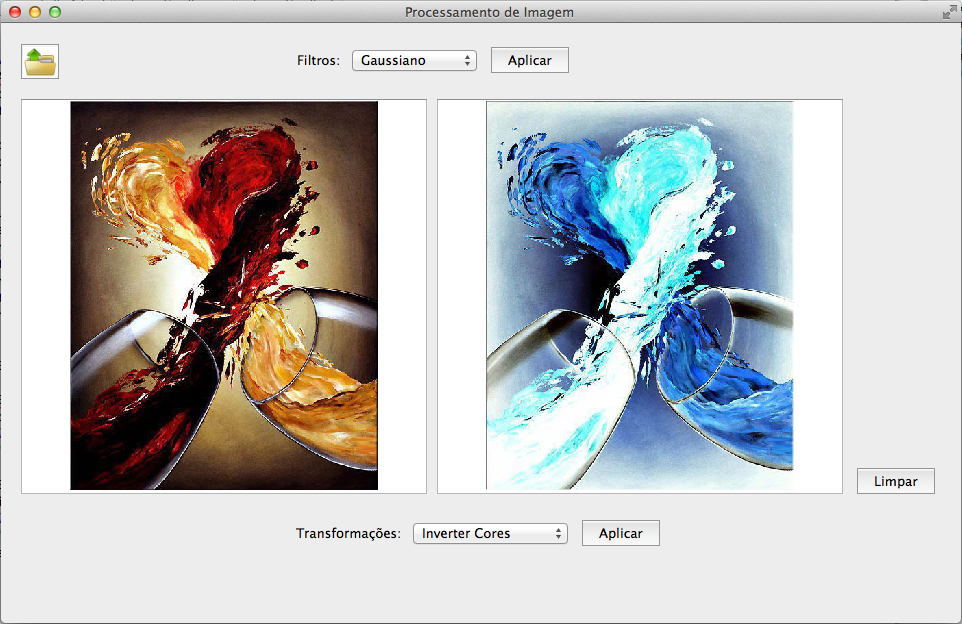
Imagem original e imagem após inversão de cores.
TONS DE CINZA: Tornar uma imagem colorida, em tons de cinza significa uniformizar cada pixel com os mesmos valores para as componentes R, G e B. Para calcular essa intensidade luminosa da cor R,G,B, intuitivamente pode-se pensar em fazer uma média aritmética entre os valores das componentes. No entanto, há equações próprias para diferentes dispositivos, que levam em consideração a sensibilidade relativa dos nossos olhos para os diferentes comprimentos de onda. A equação utilizada neste trabalho para calcular a intensidade luminosa do pixel é a utilizada para os monitores atuais: Y = 0.2126*Red + 0.7152*Green + 0.0722*Blue
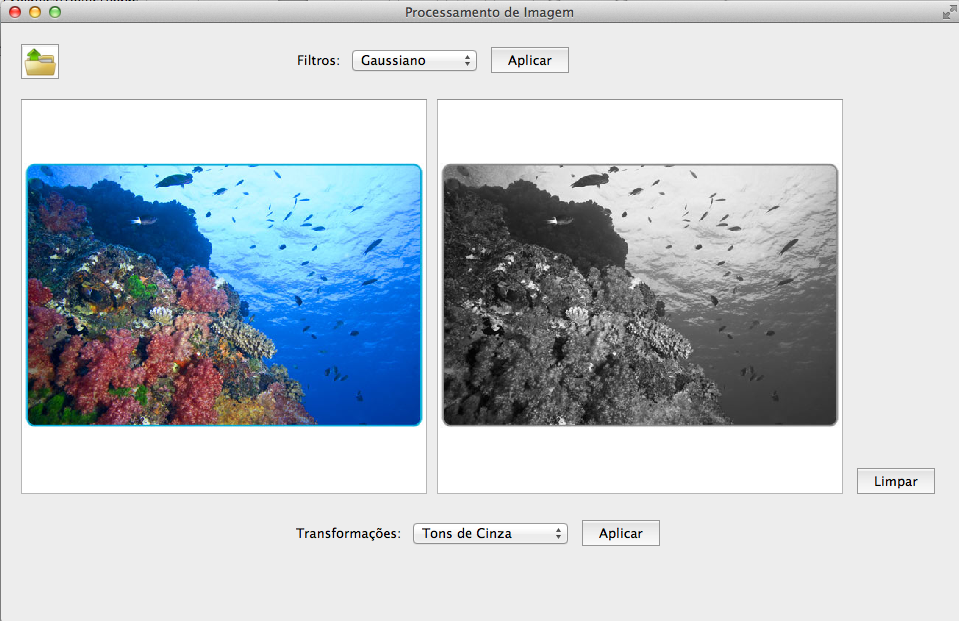
Imagem original e imagem após conversão para tons de cinza.
Raquel Jauffret Guilhon
23/06/2013
23/06/2013