Bump mapping [6], like texture mapping, is a technique to add more realism to synthetic images without adding a lot of geometry. Texture mapping adds realism by attaching images to geometric surfaces. Bump mapping adds per-pixel surface relief shading, increasing the apparent complexity of the surface.
Surfaces that should have a patterned roughness are good candidates for bump mapping. Examples include oranges, strawberries, stucco, wood, etc.
A bump map is an array of values that represent an object's height variations on a small scale. A custom renderer is used to map these height values into changes in the local surface normal. These perturbed normals are combined with the surface normal, and the results are used to evaluate the lighting equation at each pixel.
The technique described here uses texture maps to generate bump mapping effects without requiring a custom renderer [1] [49]. This multipass algorithm is an extension and refinement of texture embossing [54].
The first derivative of the height values of the bump map can found by the following process:
Consider a one dimensional bump map for simplicity. The map only varies
as a function of s. Assuming that the height values of the bump map can
be represented as a height function f(s), then the three step process
above would be like doing the following: f(s) - f(s + shift). If
the shift was by one texel in s, you would have 
,
where w is the width of the texture in texels. This
is a different form of 
which is just the basic
derivative formula. So shifting and subtracting results in the first
derivative of f(s), f'(s).
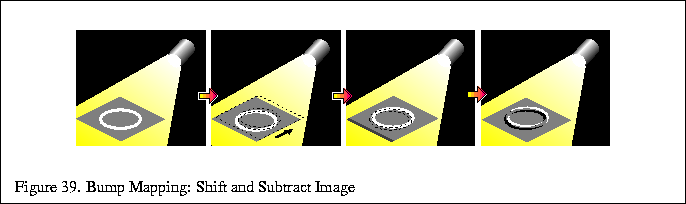
In the two dimensional case, the height function is f(s,t), and shifting and subtracting creates a directional derivative of f(s,t). This technique is used to create embossed images.
With more precise shifting of the texture coordinates, we can get general bump mapping from this technique.