8.5.1 Tangent Space

In order to accurately shift, the light source direction must be rotated into tangent space. Tangent space has 3 perpendicular axes, , and . , the tangent vector, is parallel to the direction of increasing s or t on a parametric surface. , the normal vector, is perpendicular to the local surface. , the binormal, is perpendicular to both and , and like , also lies on the surface. They can be thought of as forming a coordinate system that is attached to surface, keeping the and vectors pointing along the tangent of the surface, and pointing away. If the surface is curved, the tangent space orientation changes at every point on the surface.

 

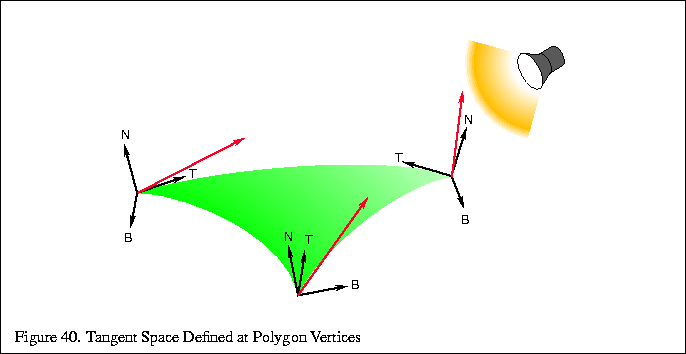
In order to create a tangent space for a surface, it must be mapped parametrically. But since this technique requires applying a 2D texture map to the surface, the object must already be parametrically mapped in s and t. If the surface is already mapped with a surface detail texture, the s and t coordinates of that mapping can be reused. If it is a NURBS surface, the s and t values of that mapping can be used. The only requirement for bump mapping to work is that the parametric mapping be consistent on the polygon. Of course, to avoid ``cracking'' between polygons, the mapping should be consistent across the entire surface.

The light source must be rotated into tangent space at each vertex of the polygon. To find the tangent space vectors at a vertex, use the vertex normal for , find the tangent axis by finding the vector direction of increasing s in the object's coordinate system (the direction of the texture's s axis in the object's space). You could use the texture's t axis as the tangent axis instead if it is more convenient. Find by computing the cross product of and . The normalized values of these vectors can be used to create a rotation matrix:

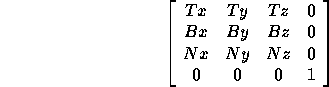
This matrix rotates the vector, defined in object space, into the x axis of tangent space, the vector into the y axis, and the normal vector into the z axis. It rotates a vector from object space into tangent space. If the , , and vectors are defined in eye space, then it converts from eye space to tangent space. For all non-planar surfaces, this matrix will differ at each vertex of the polygon.

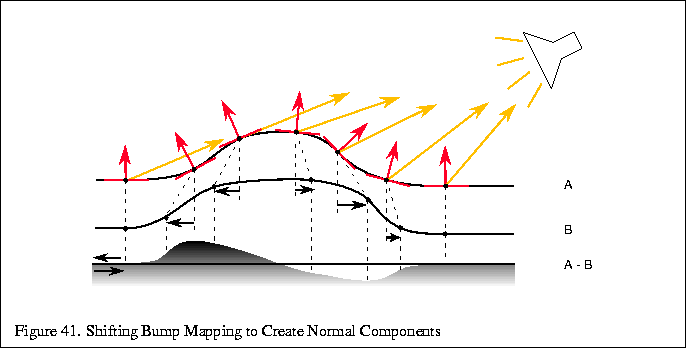
Now you can apply this matrix to the light direction vector , transforming it into tangent space at each vertex. Use the transformed x and y components of the light vector to shift the texture coordinates at the vertex.

The resulting image, after shifting and subtracting is part of computed in tangent space at every texel. In order to get the complete dot product, you need to add in the rotated z component of the light vector. This is done as a separate pass, blending the results with the previous image, but adding, not subtracting this time. It turns out that this third component is the same as adding in the Gouraud shaded version of the polygon to the textured one.

 

So the steps for diffuse bump mapping are:

1. Render the polygon with the bump map textured on it. Since the bump map modifies the polygon color, you can get the diffuse color you want by coloring the polygon with .
2. Find , and at each vertex.
3. Use the vectors to create a rotation matrix.
4. Use the matrix to rotate the light vector into tangent space.
5. Use the rotated x and y components of to shift the s and t texture coordinates at each polygon vertex.
6. Re-render the bump map textured polygon using the shifted texture coordinates.
7. Subtract the second image from the first.
8. Render the polygon Gouraud shaded with no bump map texture.
9. Add this image to result.

In order to improve accuracy, this process can be done using the accumulation buffer. The bump mapped objects in the scene are rendered with the bump map, re-rendered with the shifted bump map and accumulated with a negative weight, then re-rendered again using Gouraud shading and no bump map texture, accumulated normally.

The process can be extended to find bump mapped specular highlights. The process is repeated, this time using the halfway vector () instead of the light vector. The halfway vector is computed by averaging the light and viewer vectors . Here are the steps for finding specular bump mapping:

1. Render the polygon with the bump map textured on it.
2. Find , and at each vertex.
3. Use the vectors to create a rotation matrix.
4. Use the matrix to rotate the halfway vector into tangent space.
5. Use the rotated x and y components of to shift the s and t texture coordinates at each polygon vertex.
6. Re-render the bump map textured polygon using the shifted texture coordinates.
7. Subtract the second image from the first.
8. Render the polygon Gouraud shaded with no bump map texture, this time use instead of . Use a polygon whose color is equal to the specular color you want, .
9. Now you have , but you want To raise the result to a power, you can load power function values into the texture color table, using glColorTableSGI() with GL_TEXTURE_COLOR_TABLE_SGI as its target, then enabling GL_TEXTURE_COLOR_TABLE_SGI. With the color lookup table loaded and enabled, when you texture and blend the specular contribution to the result, the texture filtering will raise the specular dot product to the proper power. If you don't have this extension, then you can process the texel values on the host, or limit yourself to non-bump mapped specular highlights.
10. Add this image to result.

Combine the two images together to get both contributions in the image.